
图1 模型最终界面
零件返工仿真模型
一、 模型描述
一个计划中的生产系统包括5个串联的自动工作站。每个工作站的加工时间都是常数,分别为11,10,11,11和12(本习题所有时间单位都是分钟)。零件到达间隔时间为UNIFORM
(13,
15)。在每个工作站前都有一个容量无限的缓冲区,并假设所有的传输时间都是0。该生产系统比较特别的是:从工作站2一直到工作站5,零件都有可能需要被送到前一个工作站重新加工,例如,一个零件在工作站2加工完以后,零件可能返工多次。目前对所有的工作站来说,零件的返工概率是5%~10%,Witness仿真模型下载。
该模型的仿真目的是:运行时间为10
000分钟。运行6次,每次的返工概率分别为5%、6%、7%、8%、9%和10%。根据运行结果,绘制平均系统逗留时间与返工概率的关系图,在图形中标出每次运行的最大系统等待时间。
二、 模型建立
2.1 模型最终界面
模型最终界面如图1所示:

图1 模型最终界面
2.2 元素说明
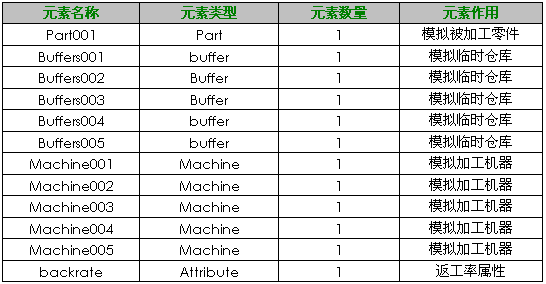
该模型中,part元素产品经过输送链conveyor元素的运输,被入库台卸载,卸载之后被储存于临时仓库(buffer元素)。再经过叉车经过四个track元素进行货架1和货架2之间的运输。具体元素详见下表:
表1 元素说明
2.3 元素可视化设计
(1)Part元素可视化设计
Part元素只有产品,只需对其name属性和style属性进行可视化设计即可。style属性选择红色圆圈图案表示。如图1所示。
(2)Buffer元素可视化设计
Buffer元素对其name属性和part queue属性可视化设计。其中part queue属性选择queue选项中的right选项。
(3) machine元素可视化设计
Machine元素需要对其icon属性、part queue属性以及icon属性(静态图标)、icon(动态图标)进行可视化设计。
2.4 元素详细设计
(1)Part元素详细设计
Part元素详细设计如图2所示:

图2 part001元素详细设计
其中,点击“To…”按钮,输入:“push to
buffers001”,表示,产品进入系统的时间间隔服从13到15之间的均匀分布。进入系统后零件将暂时保存在buffers001中。
(2)machine元素详细设计
Machine元素有5个。但是每个machine元素的详细设计基本相同。现以machine001和machine002为例介绍machine元素的设置过程。
Machine001详细设计
Machine001由于是第一台加工机器,因此,加工完零件后全部送入第二道工序前的缓冲中,没有返工这一说。详细设计如图3所示:
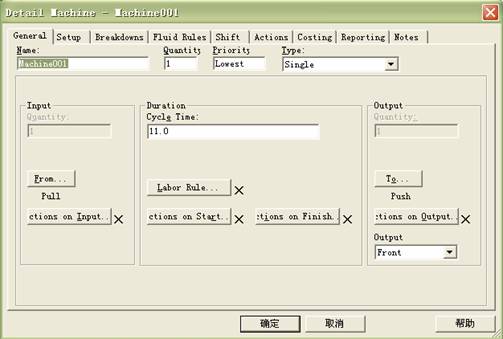
图3 machine001元素详细设计
其中, 点击“to…”按钮,输入:push to buffers002。
点击“from…“按钮,输入:pull from buffers001。
Machine002详细设计
具体设计如图4所示:
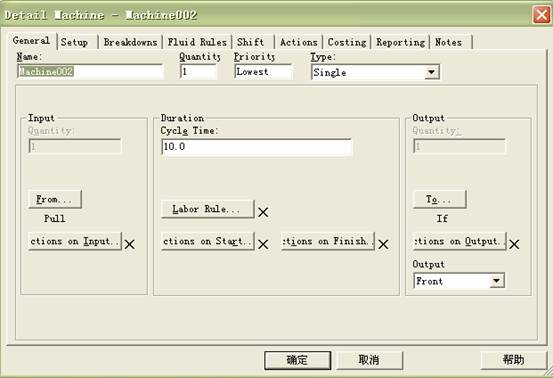
图4 machine002详细设计
其中:
“from”中输入:pull from buffers002。
“to”中输入:
IF UNIFORM (0,100) < BackRate
PUSH to Buffers001
ELSE
PUSH to Buffers003
ENDIF
注: 表示按照返工率来对产品质量进行判断,如果随机分布数是在返工率以下,说明零件不合格,需要返工,则零件运往上级工序前的缓冲区。如果大于返工率,表示产品合格,运往下道工序的缓冲区内。
Cycle time中输入10。表示加工产品时间服为10min每件。
需要注意的是:machine003、machine004都是与machine002的设置基本相同,只需要改变加工产品的时间和上道工序与下道工序的缓冲区的名称即可。
Machine005的“to“按钮中将输入:push to ship。表示最终零件将运出系统。
三、 运行模型
按照题目要求,运行时间为10
000分钟。运行6次,每次的返工概率分别为5%、6%、7%、8%、9%和10%。根据运行结果,绘制平均系统逗留时间与返工概率的关系图,在图形中标出每次运行的最大系统等待时间。
在此需要介绍返工率在该模型中如何改变。选择菜单栏中的model/initialize actions.输入:Backrate=10。!表示返工率现在界定为10%。如果每次要在不同的返工率的基础上运行程序,只需将10改成其他数据即可。
运行模型,找出每次运行结果中的产品平均逗留时间。统计数据如表2所示:
表2 系统运行数据统计
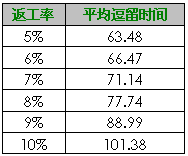

上表可以看出,随着返工率不断上升,零件在系统中逗留的平均时间也是不断上升的。